반응형
Notice
Recent Posts
Recent Comments
Link
| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | |||
| 5 | 6 | 7 | 8 | 9 | 10 | 11 |
| 12 | 13 | 14 | 15 | 16 | 17 | 18 |
| 19 | 20 | 21 | 22 | 23 | 24 | 25 |
| 26 | 27 | 28 | 29 | 30 | 31 |
Tags
- 최소 스패닝 트리
- 청년 Ai Big Data 아카데미
- codeup 1020 java
- 나누어 떨어지는 숫자 배열 java
- 최소 스패닝 트리 자바
- docker remove
- 프로그래머스 가운데 글자 가져오기 파이썬
- docker 완전 삭제
- 핸즈온 머신러닝
- m1 docker install
- 나누어 떨어지는 숫자 배열 python
- 프로그래머스 나누어 떨어지는 숫자 배열 파이썬
- m1 docker
- 빅분기실기
- 가운데 글자 가져오기 자바
- 청년 AI Big Data 아카데미 13기
- 코드업 1020 java
- 프로그래머스 가운데 글자 가져오기 자바
- 코드업 1020 자바
- 빅데이터분석기사
- 가운데 글자 가져오기 java
- codeup 1020 자바
- 트리의 지름 java
- 가운데 글자 가져오기 파이썬
- 가운데 글자 가져오기 python
- 트리의 지름 자바
- docker 삭제
- 프로그래머스 가운데 글자 가져오기 python
- 최단 경로 알고리즘
- 프로그래머스 나누어 떨어지는 숫자 배열 자바
Archives
- Today
- Total
NineTwo meet you
[선형대수] 기저 & 차원 본문
반응형
기저 basis란?
기저란 벡터 공간 V의 액기스라고 생각하면 쉽게 이해가 된다.
기저란 한가지로 정해져 있지 않지만 기저의 개수(= 차원)는 변하지 않는다.

좌표 벡터란?

표준 기저
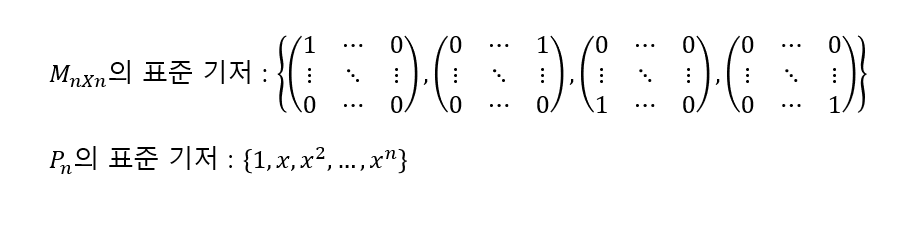
차원
벡터 공간 V가 n개의 벡터로 이루어진 기저를 갖는다면 V의 차원을 n이라한다.
V의 차원을 dimV로 표시한다.
벡터 공간 V의 기저의 원소 개수
= 벡터 공간 V의 선형 독립이 되는 최대 개수
= 벡터 공간 V의 차원
= dimV

반응형
'수학 > 선형대수' 카테고리의 다른 글
| [선형대수] 선형사상 (0) | 2021.01.27 |
|---|---|
| [선형대수] 일차 독립 & 일차 종속 (0) | 2021.01.27 |
| [선형대수] 벡터공간 Vector space (0) | 2021.01.27 |
| [선형대수] 고유치 eigenvalue 와 고유벡터 eigenvector (0) | 2021.01.27 |
| [선형대수] 랭크 Rank (0) | 2021.01.27 |
Comments




